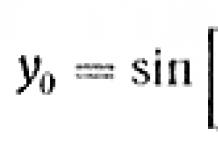Цели урока:
Обучающая
- знать формулы дифференцирования; правила дифференцирования;
дифференцирование сложной функции; физический и геометрический смысл производной;
уравнение касательной к графику функции.
Развивающая - уметь находить производные функции; решать задачи с применением физического смысла, геометрического смысла; находить значение производной функции в точке; математически грамотно объяснять и обосновывать выполняемые действия.
Воспитательная – воспитывать самостоятельность, ответственность, рефлексию.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания
(во время перемены проверяют консультанты (учащихся),с выставлением оценок).
III. Постановка цели и мотивация
Учитель сообщает учащимся о том, что данный урок является заключительным уроком по теме “Вычисление производных” и предлагает им самостоятельно сформулировать цели.
Учитель: - “Великий философ Конфуций однажды сказал: “Три пути ведут к знанию: путь размышления - это путь самый благородный, путь подражания - это путь самый легкий и путь опыта - это путь самый горький”. Так вот сегодня на уроке каждый из вас определит на каком пути к знанию данной темы он находится”.
Перед учащимися ставится задача - показать свои знания и умения по вычислению производных и сообщается план урока.
I этап:
Выполнение задания по карточке “Вспомни”.
(проверка знаний формул и правил дифференцирования).
II этап: Устная фронтальная работа на повторение и обобщение знаний.
III этап: «Тест-прогноз» (при выполнении данного задания допустима помощь консультантов).
I V этап: Решение практической задачи.
V этап: Самостоятельная работа
Оцениваются I, III, V этапы работы и домашнее задание. Проверяют и вносят результаты в оценочную таблицу консультанты.
Критерии оценок: «5»
- 19-20 баллов;
«4»
- 15-18 баллов;
«3»
- 10-14 баллов.
Пути к знанию
- Воспроизведение и коррекция опорных знаний
I этап.
Цель: контроль, самоконтроль знаний формул и правил дифференцирования
Вспомни! Ф.И. __________________________________________________ |
|
Производная |
|
c,c - const |
|
|
|
|
|
f "(x)+g "(x) |
|
f (x)*g (x) |
|
|
|
По окончанию данного задания выполняется самопроверка по “Таблице производных”. Карточки сдаются консультантам на проверку (исправление в карточках не допускаются).
V. Обобщение и систематизация знаний
II этап.
1.Устная фронтальная работа.
А. Сформировать задание к данному условию и решить его.
![]()
1. Найти значение производной функции в точке t = 3. (Ответ: 21.)
2. Составить уравнение касательной к графику функции в точке t = 3. (Ответ: у = 21х-45.).
3. Найти скорость движения тела и ускорение в момент времени t=3c , если закон движения задан формулой . (Ответ: 21м/c, 16 м/с²).
4. Найти угловой коэффициент касательной, проведенной к графику функции в точке t = 3. (Ответ: 21.).
5. Найдите тангенс угла наклона касательной к графику функции в точке t = 3 и определите вид угла между касательной и положительным направлением оси Ox. (Ответ: tgα, угол α - острый)
В. Найдите производные функций

2. III этап “Тест-прогноз”


По окончанию данного задания выполняется самопроверка по итоговым ответам и тесты сдаются консультантам. (исправление в карточках не допускаются).
Ответы:
1 вариант |
||||
2 вариант |
- Решение задачи
I
V этап
Фронтальное решение задачи повышенного уровня (решение выполняют консультанты совместно с классом).
Задача
При каких значения параметра a
касательные к графику функции
![]()
проведенные в точках его пересечения с осью X, образуют между собой угол 60°?

Графиком является парабола с ветвями вверх, пересекающие ось X в двух точках (случай a =0 не удовлетворяет смыслу задачи):
IX. Подведение итогов и выставление оценок
1. Вопросы: а) Выполнена ли цель урока?
б) Какой этап показался наиболее сложным?
в) Что было наиболее интересным?
2. Консультанты озвучивают результаты (количество и фамилия учащихся на пути
подражания, пути размышления и пути опыта).
Практические работы
по математике
1. Нахождение предела функции. Первый и второй замечательные пределы.
2. Производная сложной функции. Исследование функции одной переменной и построение графиков.
3. Контрольная работа «Применение дифференциального исчисления к исследованию функций».
4. Нахождение неопределенных интегралов. Вычисление определенных интегралов.
5. Вычисление определителей.
6. Решение систем линейных уравнений методом Крамера. Контрольная работа.
7. Решение задач по теме «Множества». Формулы алгебры логики.
8. Вычисление вероятностей случайных событий. Формула полной вероятности.
9. Вычисление числовых характеристик.
10. Контрольная работа «Основы теории вероятностей и математической статистики»
11. Тригонометрическая форма комплексного числа.
12. Действия с комплексными числами в различных формах.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ РАБОТ ПО МАТЕМАТИКЕ
2 КУРС
Практическое занятие - это форма организации учебного процесса, предполагающая выполнение студентами по заданию и под руководством преподавателя одной или нескольких практических работ .
Так, на практических занятиях по математике у студентов формируется умение решать задачи, которое в дальнейшем должно быть использовано для решения профессиональных задач по специальным дисциплинам.
В ходе практических работ студенты овладевают умениями пользоваться информационными источниками, работать с нормативными документами и инструктивными материалами, справочниками, выполнять чертежи, схемы, таблицы, решать разного рода задачи, делать вычисления.
Задачи, которые решаются в ходе практических занятий по математике:
1) расширение и закрепление теоретических знаний по математике, полученных в ходе лекционных занятий;
2) формирование у студентов практических умений и навыков, необходимых для успешного решения задач по математике;
3) развитие у студентов потребности в самообразовании и совершенствовании знаний и умений в процессе изучения математики;
4) формирование творческого отношения и исследовательского подхода в процессе изучения математики;
5) формирование профессионально-значимых качеств будущего специалиста и навыков приложения полученных знаний в профессиональной сфере.
Практическое занятие №1. Вычисление пределов функций. Первый и второй замечательные пределы.
Тема : Вычисление пределов функций.
Цель: приобретение базовых знаний в области фундаментальных разделов математики. Проверка усвоения знаний по вычислению пределов функций. Повторить и систематизировать знания по данной теме.
Задачи:
Развитие творческого профессионального мышления;
Овладение языком науки, навыки оперирования понятиями;
Овладение умениями и навыками постановки и решения задач;
Углубление теоретической и практической подготовки;
Развитие инициативы и самостоятельности студентов.
Закрепление вычислительных навыков;
Продолжить работу над математической речью.
Формирование навыков самостоятельной работы, работы с учебником, навыки самостоятельного добывания знаний;
Развитие умения выделять главное при работе с текстом;
Формирование самостоятельности мышления, мыслительных операций: сравнение, анализ, синтез, обобщение, аналогия;
Показать обучающимся роль систематической работы по углублению и повышению прочности знаний, по культуре выполнения заданий;
Развитие творческих способностей учащихся.
Обеспечение практической работы:
Теоретический материал методической рекомендации к практической работе.
Математика, – Серия: Среднее профессиональное образование . - Ростов-на-Дону «Феникс»,с.
Ход практического занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности обучающихся к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
Изучить теоретический материал по теме «Вычисление пределов функций».
Рассмотреть примеры решения типовых заданий.
Выполнить самостоятельную работу по вычислению пределов функций с использованием первого и второго замечательного пределов.
Ответить на контрольные вопросы.
Теоретические сведения и методические рекомендации
по решению задач.
1. Изложение теоретического материала.
Чтобы вычислить предел функции в точке, надо:
1) Подставить вместо переменной x то, к чему x стремится.
2) Если после выполнения пункта 1) получим неопределенность вида https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">а стрелку заменить на минус: (x-а).
3) Если после выполнения пункта 1) получим неопределенность вида https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src=">, связанная с значениями тригонометрических функций, надо воспользоваться первым замечательным пределом.
Определение. Первым замечательным пределом называется предел
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_{x\to0}\dfrac{\sin x}{x}=1.$" width="102" height="52">
5) Определение: Вторым замечательным пределом называется предел

Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число называют основанием натуральных логарифмов (https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:
![]()
2. Закрепление изученного материала.
Пример 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Мы воспользовались правилом 1) и подставили вместо x то, к чему x стремиться, т. е. x=2.
Пример 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">=5
Пример 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">.png" width="138" height="24 src=">=3+3=6
Пример 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">.png" height="30 src=">
Пример 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Пример 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
б) 
в) 
3. Закрепление знаний, умений и навыков.
Выполнить самостоятельную работу по вычислению пределов функций.
Практическая работа №1. Вариант 1 Вычислите предел функции: 1. 2. 3. 10. | Практическая работа №1. Вариант 2 Вычислите предел функции: 1. 2. 3. 10. |
Практическая работа № 2.
Тема : Нахождение производной функции. Исследование функции одной переменной и построение графика.
Цель : Проверить на практике знание понятия производной функции, умение находить производные элементарных функций, сложных функций, обратных функций, пользуясь таблицей производных и правилами дифференцирования, понятием сложная и обратная функция, умение применять производную для исследования функций.
Обеспечение практической работы :
Учебник. «Математика». – М.: Дрофа, 2010.
Математика. М:Форум-Инфа 2008.
Индивидуальные карточки с вариантом практической работы.
1.Теоретический материал и примеры нахождения производной функции.
Определение: Производной функции f(x) (f"(x)) в точке x называется предел отношения приращения функции к приращению аргумента при приращении аргумента стремящемся к нулю:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (С·u)′=С·u′, где С=соnst
5..png" width="49" height="54 src=">
6. Производная сложной функции:
f′(g(x))=f′(g)·g′(x)
2. Примеры.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src=">.png" width="69" height="41 src=">+4).
Функция представляет собой произведение двух множителей: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width="64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Функция представляет собой частное двух выражений: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width="215" height="57 src=">.png" width="197 height=36" height="36">
Решение. Найдем производную данной функции по правилу дифференцирования сложной функции (формула 6):

5. Если , то 
6. y = x 3 – 3x 2 + 5x + 2. Найдем y "(–1).
y " = 3x 2 – 6x + 5. Следовательно, y "(–1) = 14.
7. Если y = ln x · cos x , то y " = (ln x ) " cos x + ln x (cos x ) " =1/x ∙cos x – ln x · sin x.
Пусть дана функция. Для её исследования нужно:
1) Найти её область определения. Если это не слишком сложно, то полезно найти также область значений. (Однако, во многих случаях, вопрос нахождения откладывается до нахождения экстремумов функции.)
2) Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной, не является ли она периодической.
3) Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения, если такие граничные точки имеются. Если функция имеет точки разрыва, то эти точки тоже проверить на наличие вертикальных асимптот функции. Найти наклонные асимптоты.
4) Найти точки пересечения графика с осями координат, что состоит в простом вычислении значения функции при условии:
С осью ОX: y=0;
С осью ОY: x=0.
Нахождение точек пересечения с осью может привести к необходимости решить сложное алгебраическое уравнение, что, быть может, удастся сделать лишь приближённо. Отыскав корни функции и точки разрыва, мы можем определить знак функции на каждом из интервалов между этими точками. Это можно сделать либо вычислив значение функции в какой-нибудь из точек интервала, либо применив метод интервалов.
5)Найти промежутки монотонности. Для этого находят производную и решают неравенство:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, функция убывает.
Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума: там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием - локальные минимумы.
6) Нахождение интервалов выпуклости и вогнутости ведётся с помощью второй производной..png" width="39" height="19 src="> на интервалах:
если https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, то кривая графика функции выпуклая.
Заодно определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).
7) Нахождение точек пересечения графика с асимптотой и дополнительных точек. Этот пункт не носит обязательного характера, однако нахождение таких точек придаёт исследованию функции и построенному её графику законченность и полноту.
Заметим, что получающиеся в процессе исследования функции точки на осях координат и на графике полезно сразу же наносить на чертёж. Это помогает по ходу дела уяснять вид графика.
3. Выполните самостоятельно:
|
варианта | Найти производную функции y: |
варианта | Найти производную функции y: |
1. y=6- | 1. y=-6- 5. y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Практическое занятие
Тема: Нахождение производных. Применение производной к исследованию функции и построению графиков.
Цель: Освоить вычисление производных, научиться исследовать функцию с помощью производной
Средства обучения: тетради для выполнения практических занятий, презентации по теме, Интернет-ресурсы.
1. Рассмотрите теоретический материал по темам: «Правила вычисления производных», «Экстремум функции», «Выпуклость, вогнутость. Точка перегиба».
2. Рассмотрите образцы выполнения заданий.
3. Выполните тестовое задание №.1.
Контрольные вопросы:
1. Дайте определение максимума (минимума) функции в точке. Что можно сказать о знаке приращения функции в достаточно малой окрестности точки максимума (минимума)?
2. Каковы необходимые условия существования экстремума функции? Каков их геометрический смысл?
3. Каково правило нахождения наибольшего и наименьшего значений функции на отрезке?
4. Дайте определение выпуклости (вогнутости) кривой на промежутке.
5. Каково правило отыскания интервалов выпуклости и вогнутости кривой?
6. Точка перегиба кривой. Как ее найти?
7. Каков алгоритм построения графика функции?
Правила вычисления производных
Производная сложной функции.
Если у =ƒ(и ), и=φ (х), то у ¢ (х )=ƒ¢ (и)·φ ¢ (х ).
Производная суммы .
Если у (х )=и (х )+v (х ), то у ¢ (х )=и ¢ (х )+v ¢ (х )
Производная произведения.
Если у(х)=и (х )·v (х ), то у ¢ =и ¢ · v + u · v ¢ .
В частности, (с ·и) ¢ =с ·и ¢ , т. е. постоянный множитель выносится из-под знака производной. Легкоубедиться, что
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 ·u ¢ , … , (u n ) ¢ =n·u n–1 ·u ¢ .
Производная частного .
Если , то  .
.
Таблица производных
1. (с) ¢ =0
Для сложной функции: если и=и(х) , то:
2. (х) ¢ =1
3. (х α )¢ =α ·х α–1 , а – любое действительное число.
 .
.
3. 

4. (а х ) ¢ =а х · ln а
4. 
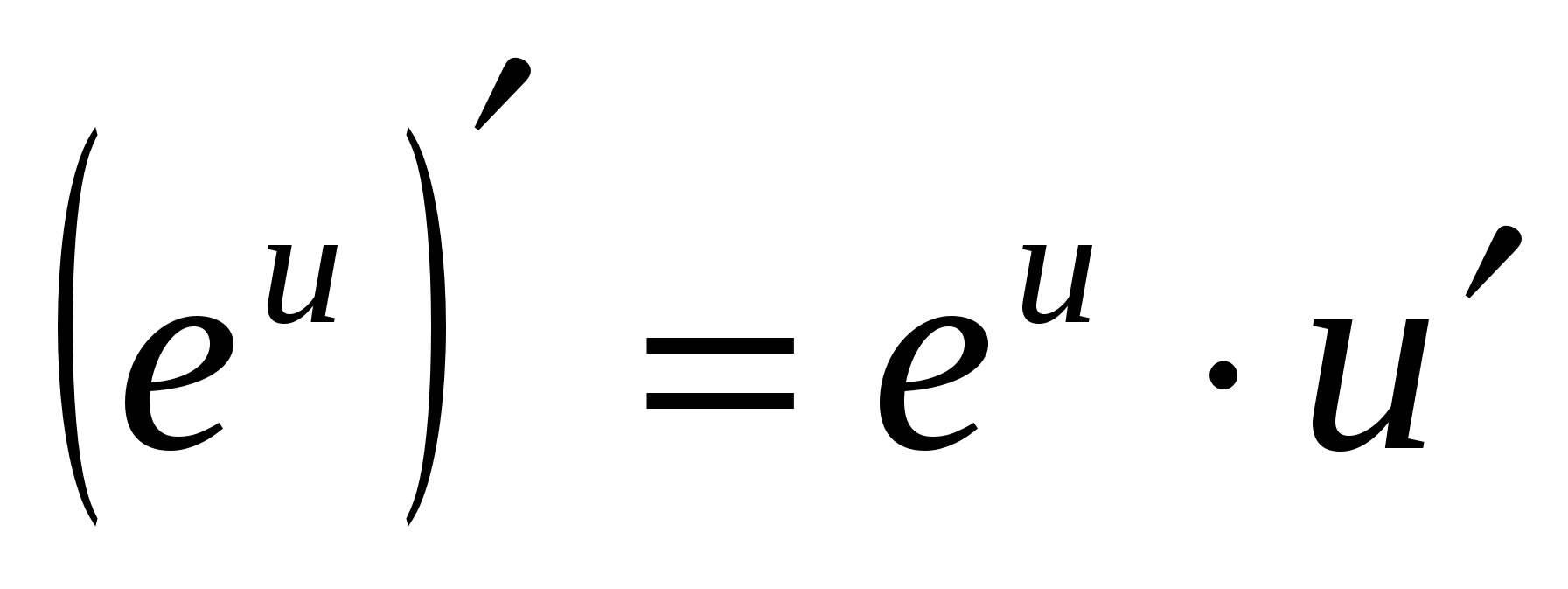
5. (log
a
x)
¢
=
 .
.
5. 

6. (sin x) ¢ =cos x
6. 
7. (cos x) ¢ = –sin x
7. 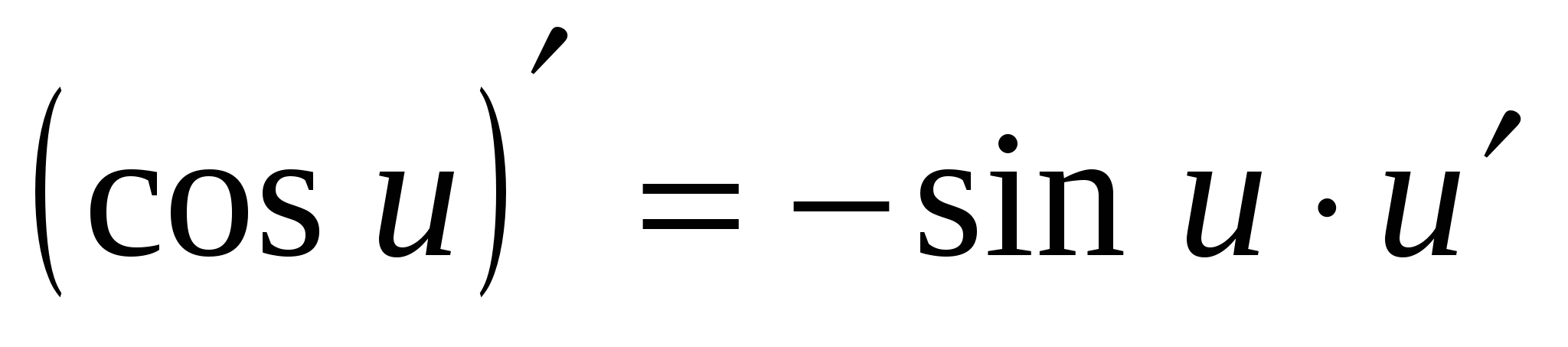
8. (tg x)
¢
=
8. 
9. (ctg x)
¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
Рассмотрите примеры
Пример 1.
у=(3–2 sin 5x ) 4 | Применяем формулы производных для и α , sin u |
y ¢ =4·(3–2·sin5x) 3 ·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Пример 2.
. 

Пример 3.
 .
. 

Пример 4.



Пример 5.
 .
. 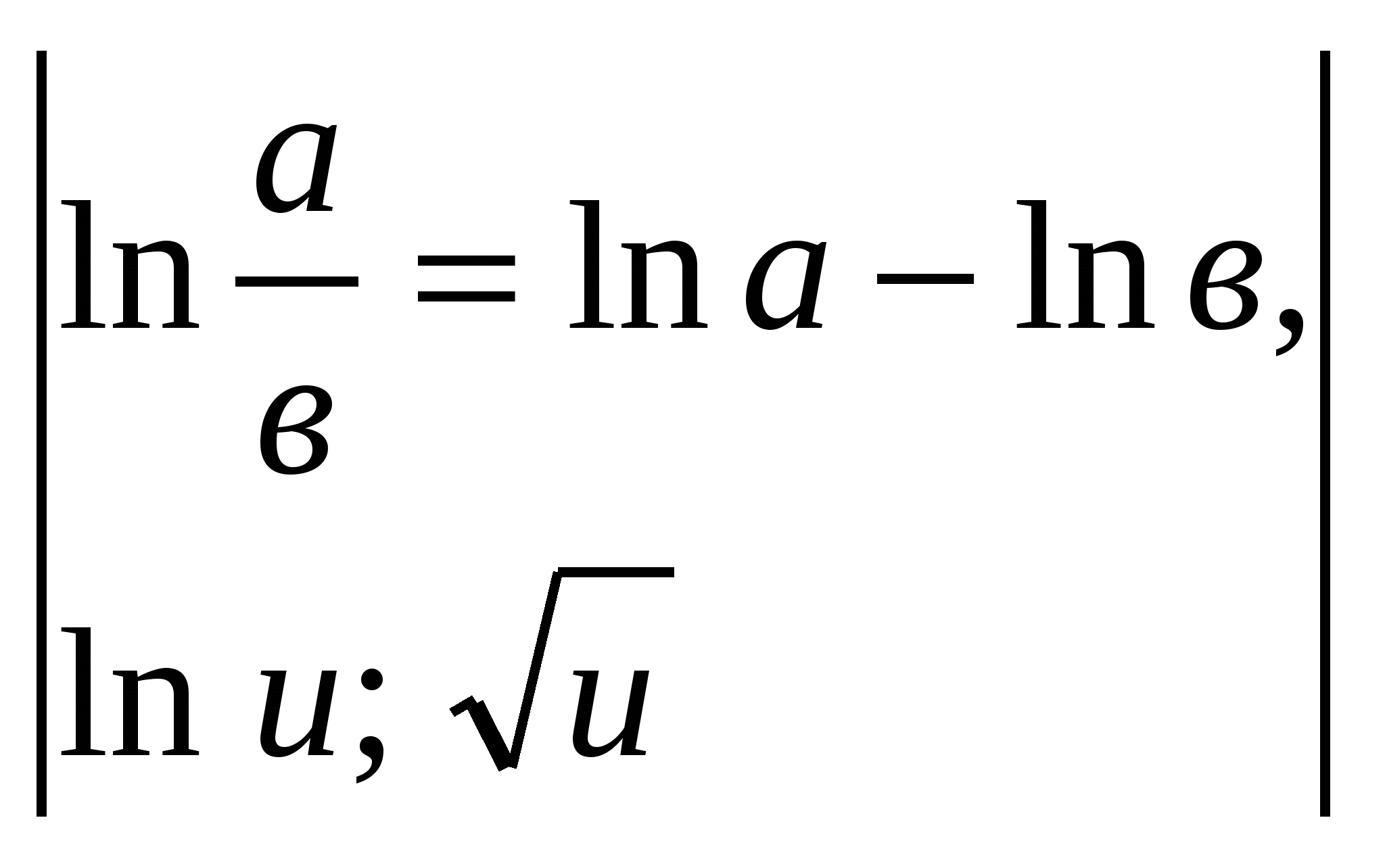

Экстремум функции
Исследование функции на экстремум – одно из важнейших приложений производных. Рассмотрим определение минимумов и максимумов, и способы их отыскания.
Пусть функция ƒ(х ) определена и дифференцируема на некотором множестве и точка х 0 – точка внутри него.
Определение. Функция ƒ (х ) в точке х 0 имеет максимум (минимум), если существует такая окрестность точки х 0 , что для всех х из этой окрестности ƒ (х ) < ƒ (х 0 ) (ƒ (х ) > ƒ (х 0 )).
Точка х 0 называется тогда точкой максимума (минимума).

Рис. 1.
Показан график функции, которая имеет две точки максимума (х 1 и х 3) и две точки минимума (х 2 и х 4), причем максимальное значение может оказаться меньше минимального (ƒ (х 1 ) < ƒ (х 4)). Это подчеркивает тот факт, что мы характеризуем особенность функции только вблизи некоторой точки.
Значения функции в точках максимума и минимума называют экстремальными значениями или экстремумами . На приведенном графике видно, что точки экстремума (х 1 , х 2 , х 3 , х 4) определяют интервалы монотонности функции, в каждом из которых производная сохраняет определенный знак. В точках экстремума, понятно, производная обращается в нуль. Сформулируем теорему о необходимом условии существования экстремума .
Теорема. Если функция ƒ (х ) в точке х 0 имеет экстремум, то производная функции в этой точке равна нулю, т. е. ƒ¢ (х 0)=0.
Заметим сразу, что условие это не является достаточным, т. е. обратное утверждение не всегда верно. Из равенства ƒ ¢ (х 0)= 0 не обязательно следует, что в точке х 0 существует экстремум.
Подтверждением тому пример с функцией ƒ (х )=х 3 .
Найдем ƒ ¢ (х )= 3х 2 . В точке х =0 ƒ ¢ (0)=0. Но как угодно близко к точке х =0 найдем х > 0, где ƒ (х )=х 3 > 0, найдем х < 0, где ¦ (х )=х 3 < 0. Т. е. не существует какая-либо малая окрестность точки х =0, где для всех х значение функции в точке х =0 будет самым большим или самым малым. Поэтому точка х =0 не является точкой экстремума.
Можно рассуждать иначе. Так как производная ƒ ¢ (х)=3х 2 , то функция ƒ(х)=х 3 возрастает при любых действительных х и экстремумов не имеет.
Точки, в которых выполняется необходимое условие экстремума (ƒ ¢ (х)=0) называются критическими .
Очевидно, что касательная к графику функции в точках, где ƒ¢ (х)=0, параллельна оси абсцисс Ох.
Достаточное условие экстремума дается в следующих теоремах.
Теорема 1. Если х 0 – критическая точка функции и при переходе через нее производная меняет знак, то х 0 – точка экстремума, а именно, если производная меняет знак с плюса на минус – точка максимума, если – с минуса на плюс – точка минимума.
Заметим, что экстремума в точке нет, если производная не меняет знака. Правило исследования на экстремум с помощью первой производной известно из школьного курса. Достаточное условие экстремума иногда удобнее формулировать с помощью второй производной.
Пусть функция ƒ(х ) дважды дифференцируема в некоторой области (т. е. ƒ(х ) имеет ƒ¢ (х ) и ƒ ¢¢ (х )).
Теорема 2. Если х 0 – критическая точка функции ƒ(х) и ƒ¢¢ (х 0 ) > 0 , то х 0 – точка минимума, если ƒ ¢¢ (х 0 ) < 0, то х 0 – точка максимума.
С помощью второй производной определяется выпуклость или вогнутость графика функции.
Выпуклость, вогнутость. Точка перегиба.
Кривая у=ƒ (х ) называется выпукло й ниже любой ее касательной
ƒ¢¢ (х ) < 0.
Кривая у=ƒ (х ) называется вогнутой на интервале, если все точки кривой лежат выше любой ее касательной на этом интервале. Тогда на этом интервале
ƒ¢¢ (х) > 0
Определение. Точкой перегиба кривой называется точка, по одну сторону от которой кривая выпукла, по другую вогнута.
В точке перегиба ƒ ¢¢ (х )=0.
Итак, знак второй производной (как и знак самой функции и ее первой производной) свидетельствует об особенностях графика функции. Еще раз остановимся на них.
Если для всех х на интервале (а , b ) ƒ (х ) > 0 (ƒ (х ) < 0), то график лежит выше (ниже) оси абсцисс.
Если для всех х на интервале (а , b ) ƒ ¢ (х ) > 0 (ƒ ¢ (х ) < 0), то функция на (а , b ) возрастает (убывает).
Если для всех х на интервале (а , b ) ƒ ¢¢ (х ) > 0 (ƒ ¢¢ (х ) < 0), то график на (а , b ) вогнут (выпукл).
Уравнение ƒ(х )=0 определяет «нули» функции, т. е. точки пересечения графика с осью Ох.
Уравнение ƒ ¢ (х )=0 определяет критические точки.
Уравнение ƒ ¢¢ (х )=0 определяет возможные точки перегиба.
Схема исследования функции
Для исследования функции ƒ (х ) и построения графика у=ƒ (х ) следует найти:
1) область определения функции и точки пересечения графика с осями координат;
2) интервалы монотонности;
3) точки экстремумов и значения функции в этих точках;
4) интервалы выпуклости и вогнутости графика;
5) точки перегиба графика;
6) построить в декартовой системе координат все полученные точки (иногда, для уточнения графика, получают дополнительные точки) и сам график.
Наименьшее и наибольшее значения функции на отрезке
При решении некоторых задач метода оптимизации важно уметь находить наименьшее или наибольшее значения функции на некотором отрезке. Эти значения функция достигает либо в критических точках, либо на концах отрезка.
Схема отыскания наименьшего и наибольшего значений функции ƒ (х ) на отрезке [а , b ].
1. Найти производную функции ƒ ¢ (х ).
2. Найти критические точки из уравнения ƒ ¢ (х )=0.
3. Выбрать те критические точки, которые принадлежат данному отрезку [а , b ] и найти значение функции ƒ (х ) в каждой такой точке.
4. Вычислить значения функции ƒ (х ) на концах отрезка: ƒ(а ) и ƒ(b ).
5. Из полученных значений функции выбрать самое большое (наибольшее) и самое малое (наименьшее).
Пример 2.
Найти наибольшее и наименьшее значения функции ƒ(х) =х 3 –9х 2 +24х–10 на отрезке .
1. ƒ ¢ (х )= 3х 2 – 9·2х 2 + 24.
2. ƒ¢ (х )=0, 3(х 2 –6х +8)=0, х 1 =2, х 2 =4.
3. Точка х 2 =4 не принадлежит отрезку . Поэтому вычислим значение функции только в точке х 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Значения функции на концах отрезка: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Получены значения:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Наибольшее значение равно 10 и достигается в точке х =2. Наименьшее – равно –10 и достигается в точке х =0.
Пример 3.
Найти интервалы выпуклости и вогнутости и точки перегиба кривой у=х +36х 2 –2х 3 –х 4 .
Областью определения данной функции является множество всех действительных чисел, т. е. х Є(–∞, +∞).
Найдем вторую производную.
у ¢ =1+72х –6х 2 –4х 3 .
у ¢¢ =72–12х –12х 2 = –12(х 2 +х –6).
Из уравнения у ¢¢ =0 получим абсциссу точки перегиба:
–12(х 2 +х –6)=0 х 1 = –3; х 2 =2.
Определим знак у ¢¢ на интервалах
(–∞; –3), (–3; 2), (2, +∞).
х
(–∞, –3)
(–3; 2)
(2; +∞)
у ¢¢
форма кривой
выпуклая
перегиб
вогнута
перегиб
выпуклая
Найдем ординаты точек перегиба:
у (–3)=726; М 1 (–3; 726) – точка перегиба
у (2)=114; М 2 (2; 114) – точка перегиба.
На интервале (–3; 2) кривая вогнута. На интервалах (–∞; –3) и (2; +∞) – выпуклая.
Образцы выполнения заданий
Задача № 1.
Найти точки разрыва функции и построить график

Функция ƒ (х ) определена для всех действительных х и непрерывна на каждом из указанных промежутков: (–∞; –1), [–1; 0], (0, +∞). Исследуем функцию ƒ (х ) на непрерывность в точках х = –1 и х =0.
Для этого в каждой из этих точек найдем односторонние пределы.

Так как односторонние пределы различны, то х = –1 – точка разрыва первого рода .

Односторонние пределы равны, т. е. в точке х=0 существует предел функции и 
Сравним этот предел со значением функции в точке: 
Так как  то в точке х=0 функция ƒ(х) непрерывна.
то в точке х=0 функция ƒ(х) непрерывна.
Построим график функции ƒ(х) , учитывая, что
1)  – уравнение прямой,
– уравнение прямой,
2)  – уравнение верхней полуокружности
– уравнение верхней полуокружности  с центром в начале координат и радиусом, равным единице, а при условии –1 £
х
£
0 уравнение
с центром в начале координат и радиусом, равным единице, а при условии –1 £
х
£
0 уравнение  определяет четверть окружности.
определяет четверть окружности.
3) для х
>
0 график задается уравнением  . Точки пересечения этой кривой с осью Ох найдем из уравнения
. Точки пересечения этой кривой с осью Ох найдем из уравнения  при х >
0. х=π
n
, где n
=1, 2, 3, 4,
при х >
0. х=π
n
, где n
=1, 2, 3, 4,

Рис. 2.
Задача № 2.
Составить уравнения касательных к линии  в точках, где х
=0 и х
=4. Найти точку пересечения касательных и угол между ними. Сделать чертеж.
в точках, где х
=0 и х
=4. Найти точку пересечения касательных и угол между ними. Сделать чертеж.
Уравнение касательной к линии у=ƒ(х) имеет вид
где у 0 =ƒ(х 0).
В точке х =0 у (0)=ƒ(0)=5.
у ¢ =ƒ ¢ (х) =х –3 ƒ¢ (0)= –3.
М 1 (0, 5) имеет вид у– 5= –3(х –0) или
у= –3х +5.
В точке х =4 у (4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Уравнение касательной в точке М 2 (4, 1) имеет вид у– 1=х –4 или
у=х –3.
Точку пересечения касательных получим, решив систему

Точка пересечения М 3 (2, –1).
Угол φ между касательными найдем из формулы:
 ,
,
где k 1 = –3; k 2 =1 – угловые коэффициенты касательных.
 .
.
Угол φ =arctg 2.
Построим данную линию  – параболу с вершиной в точке, где х
=3, т. к. у
¢
=0 при х
=3. Найдем
– параболу с вершиной в точке, где х
=3, т. к. у
¢
=0 при х
=3. Найдем  . Точка М
4 (3;
. Точка М
4 (3;  ) – вершина параболы.
) – вершина параболы.
Р
ис. 3.
Задача № 3.
Исследовать функцию 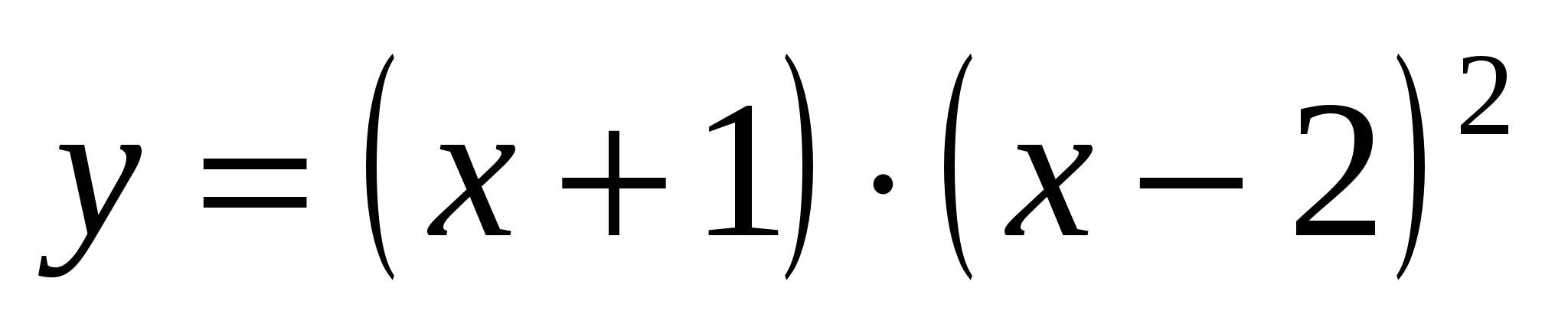 и построить ее график.
и построить ее график.
1. Данная функция является многочленом (можно раскрыть скобки, получим многочлен третьей степени), поэтому она определена, непрерывна и дифференцируема при любых х .
2. Найдем производную.
 .
.
Из уравнения у ¢ =0 найдем критические точки: 3х ·(х –2)=0, х 1 =0, х 2 =2.
Исследуем их.
х
(–∞, 0)
(0; 2)
(2; +∞)
у¢
у
3. Итак, функция возрастает на интервалах (–∞, 0) и (2, +∞), убывает на интервале (0; 2), имеет максимум при х=0 и минимум при х=2:
у max =у (0)=4; у min =у (2)=0.
4. Найдем вторую производную.
у ¢¢ = 6·(х -1).
Кривая выпукла там, где у ¢¢ < 0, т. е. 6·(х –1) < 0, х < 1.
Кривая вогнута там, где у ¢¢ > 0, т. е. х > 1.
Итак, на интервале (–∞, 1) кривая выпукла; а на интервале (1, +∞) – вогнута.
5. Точку перегиба найдем из уравнения у ¢¢ =0. Таким образом, х =1 – абсцисса точки перегиба, т.к. эта точка разделяет интервалы выпуклости и вогнутости кривой. Ордината точки перегиба: у (1)=2.
График функции у =(х +1)·(х –2) 2 пересекает ось Ох при у =0, т. е. при х = –1 и х =2;
пересекает ось Оу при х =0, т. е. при у =4. Мы получили три точки: (–1; 0), (2; 0), (0; 4). Все полученные точки внесем в таблицу, добавив соседние с ними.
–2
–1



–16


ис. 4 Кривая у=(х+1)(х–2) 2 .
Задание № 1
Вашему вниманию предлагаются задания, в которых могут быть один, два, три и большее число правильных ответов. Обвести кружочком номера всех правильных ответов
1. Если  то функция
то функция
1) возрастающая
2) убывающая
3) постоянная
2. Если
1) Возрастающая
2) Убывающая
3. Если  , то функция
, то функция
1) Возрастающая
2) Убывающая
4. Если  , то функция
, то функция
1) Возрастающая 3) Убывающая
2) Постоянная 4) Монотонная
5. Функция  Является
Является
1) Чётной
2) Не чётной
3) ни чётной, ни нечётной
4) Периодической
5) Не периодической
6) Тригонометрической
7) Элементарной
6. Функция  Является
Является
1) чётной
2) нечётной
3) ни чётной, ни нечётной
4) периодический
5) не периодической
6) тригонометрической
7) элементарной
2) Вейерштрасс 4) Дирихле 6) Лейбниц
8) Решение  Уравнения
Уравнения
1) 0 3) 0 и 3 5) 2 7) 3
2) 2 и 3 4) 2 6) -5 и 1 8) 5 и 1
9) решение неравенства 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 
10) Методом  Находится сумма
Находится сумма
1) векторов
2) прямых
3) отрезка
11) Если  , то функция
, то функция
1) Вогнутая 3) Выпуклая 5) Убывающая
2) Монотонная 4) Возрастающая 6) Постоянная
12) область определения функции равна 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 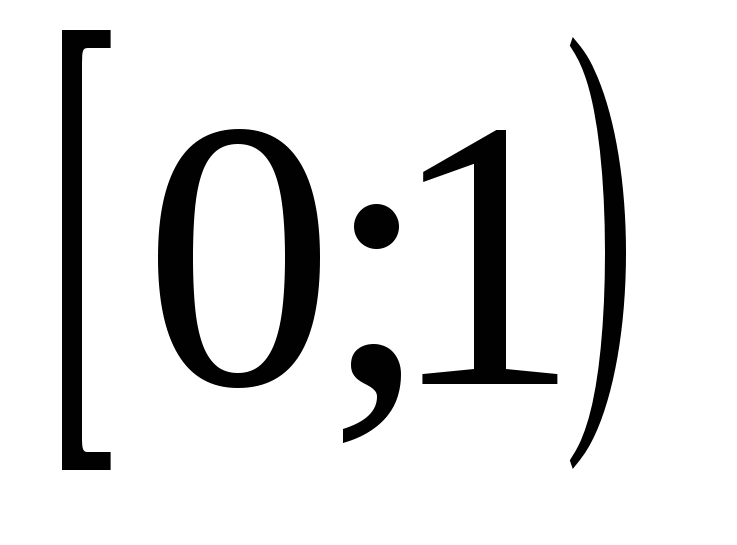
13) функция  является
является
1) показательной
2) тригонометрической
3) степенной
4) логарифмической
14) если функции у=x то она является
то она является 
1) чётной
2) нечётной
3) ни чётной, ни нечётной
15) функция  при
при  является
является

 .
.